Select the polymorph with attributes fit for development.

It is well established that polymorphism is common in pharmaceutical active ingredients.1 Bernstein and others present statistics that, when they are appropriately screened up to three in four compounds display polymorphism.2 Because of their distinct physical and chemical property differences, polymorph control becomes an essential task during drug discovery and development.3-4 Although computational predictions continue to gather attention, the formation of polymorphs still cannot be effectively predicted and must be physically screened. The screening approach at Improved Pharma attempts to answer three key questions that help select the polymorph to manufacture and formulate into a dosage form:

  1. How many polymorphs can be identified?
  2. Which form is the thermodynamic stable polymorph at room temperature?
  3. If enantiotropic pairs exist, what are the transition temperatures?

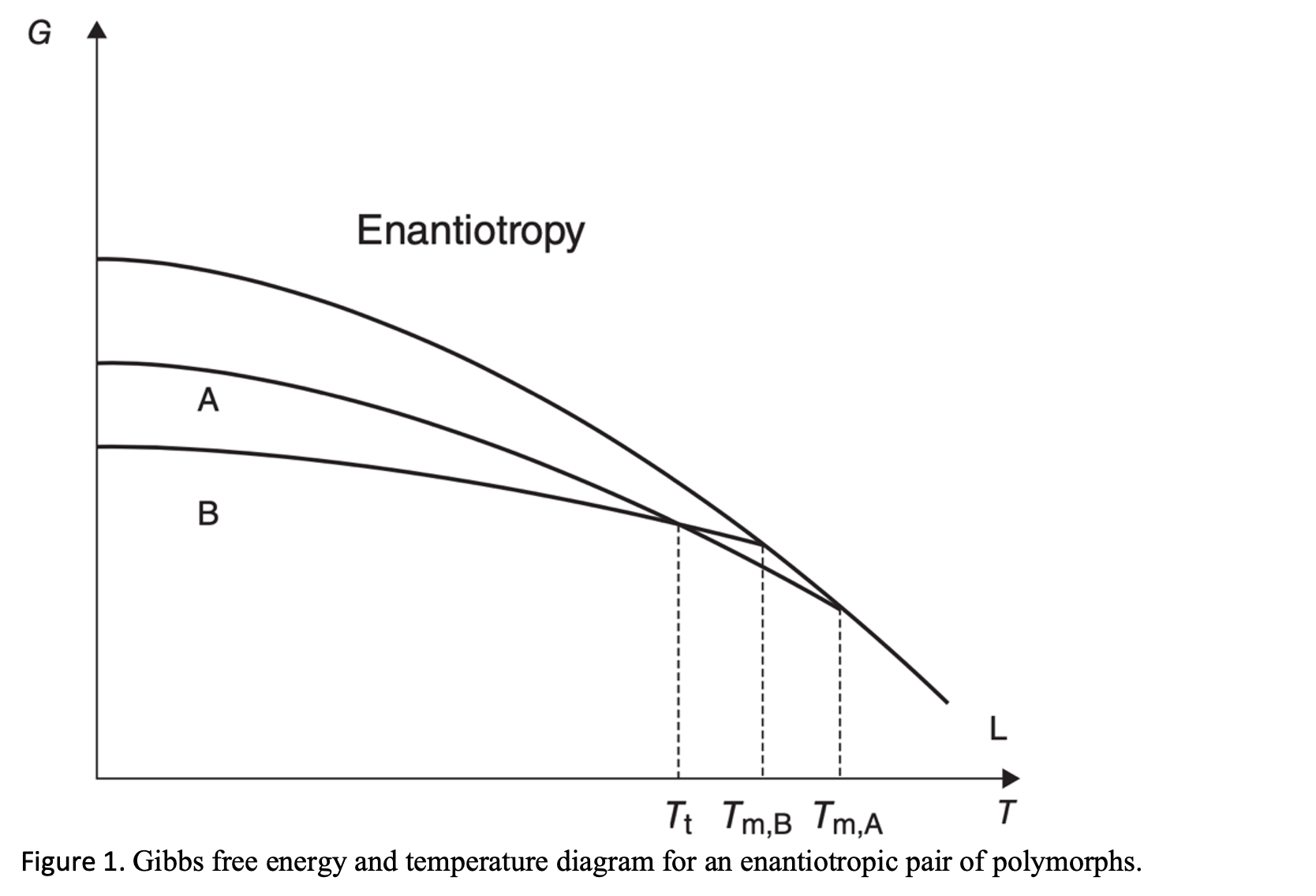The formation of polymorphs is primarily governed by the underlying thermodynamics of the system. Chapter 2 of Solid-State Properties of Pharmaceutical Materials by Byrn, Zografi, and Chen (Wiley, 2017) reviews the various structural and thermodynamic principles in pharmaceutical polymorphism.

Can you ensure polymorph control?

The relative stability of polymorphs is determined by their relative Gibbs free energy, the more stable form having the lower free energy. For a monotropic pair of polymorphs, the relative stability will stay the same below the melting point. Conversely, an enantiotropic system has a transition point below the melting temperature so that the order of the stability for the low-temperature and high-temperature polymorphic pair changes above and below the transition temperature.

There is always a thermodynamic tendency for the metastable form to change to the stable form. Monotropic transitions are irreversible, but enantiotropic transitions are reversible. Consequently, to ensure polymorph control of your API, the temperature at which the thermodynamic transition occurs between an enantiotropic pair must be identified.

The best method to determine relative stability.

Burger and Ramberger proposed several rules, based on both thermodynamic and statistical mechanics, which are useful qualitatively.5-7 The van’t Hoff plot provides a quantitative way to model stability order and transitions over a narrow temperature range.8-9 Yu has also demonstrated that the ∆G/temperature diagram constructed from calorimetric data could offer quantitative information about the relative stability of polymorphs.10 A popular approach of triturating polymorphic pairs in a suspension takes advantage of the solubility dependence on temperature.

When slow kinetics is an issue.

Some metastable forms can be stable for years whereas others are only present transiently. How the transformation occurs is determined by the kinetics of the process. Often, there are significant deviations from ideal thermodynamic behavior. Numerous studies provide examples of compounds that, due to kinetic barriers, display reversible transitions with significant hysteresis.11-15

When hysteresis occurs, the apparent transition temperature in the solid-state now depends greatly on the rate and direction of the temperature change. The result can appear considerably higher than the true thermodynamic transition temperature for the system.

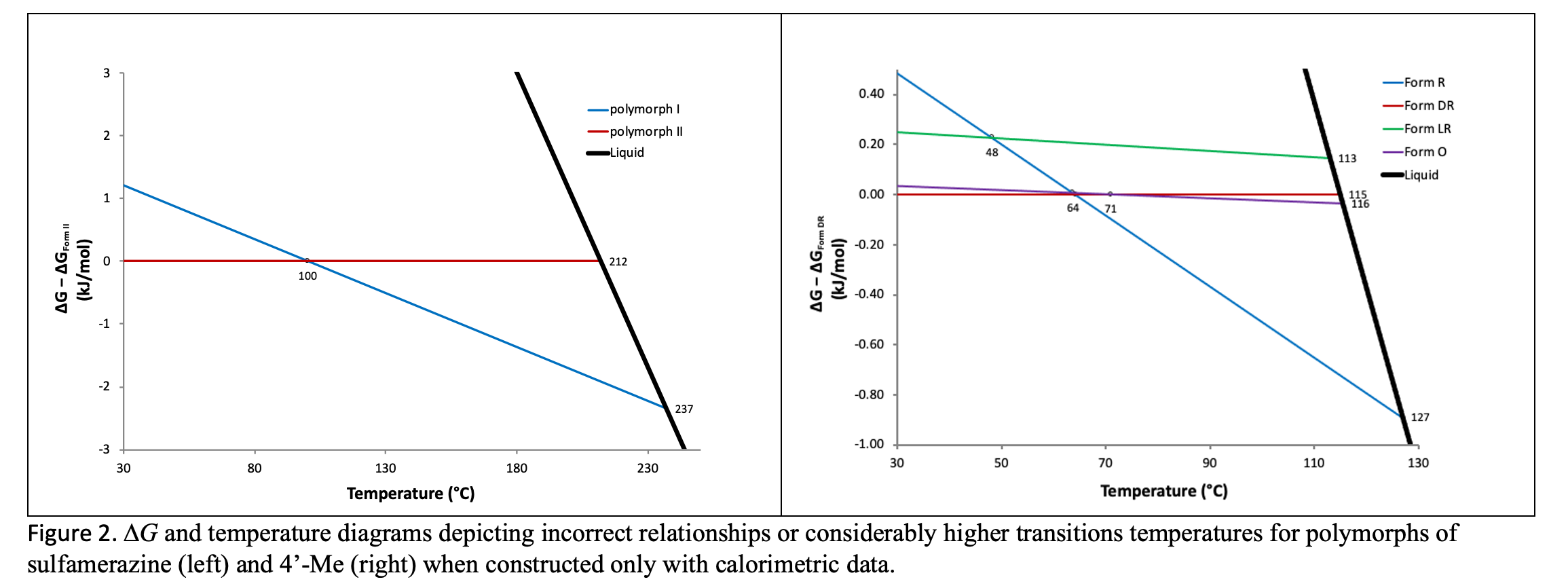
Zhang et al characterized the two enantiotropes of sulfamerzine and found that although polymorph II converts to polymorph I on heating, polymorph I does not convert back to II on cooling in the dry state.14 The apparent lack of reversibility was explained by slower kinetics of conversion at lower temperatures.7,16 Consequently, the ∆G/temperature diagram17-18, Figure 2 below (left), constructed from calorimetric data14 predicts a transition temperature near 100 °C. The true thermodynamic transition temperature was revealed to lie between the bracketing temperatures of 51 and 54 °C via solvent-mediated interconversion experiments.

Byrn found that three of the four modifications of 4’-Me exhibit melting temperatures and transitions enthalpies that were extremely close to each other.15 This led to very similar solubilities and slow transformation kinetics. Again, using only calorimetric data15 to construct the ∆G/temperature diagram17‑18, Figure 2 below (right) incorrectly predicts monotropic relationships among two polymorphic pairs of 4’‑Me and an excessively high transition temperature between a third. The characterization of the system required the application of a variety of methods to determine that all forms are enantiotropically related with six transitions points between the polymorphic pairs.

Map the relative stability of polymorphs with confidence.

Care must be taken when interpreting results based on solid-state data and should be verified with an orthogonal method. Kinetic hindrances observed in the solid-state can be mitigated with a solution-mediated mechanism using solvents with moderate solute–solvent interaction and high solubility.19 If necessary, the ∆G/temperature diagram can be constructed from solubility dependence on temperature. Improved Pharma can utilize many qualitative or quantitative approaches to investigate the relative stability of polymorphs.

In summary, determining relative stability can be complicated. It demands significant resources to establish the full relationship. The correct determination of the stability relationships among polymorphs is necessary to avoid serious scientific, regulatory, and economic consequences. The approach at Improved Pharma can include thermal analyses, solubility tests, and interconversion studies that are necessary to provide you with a map to guide drug development and preserve intellectual property.

Want to find out more?
Contact us at info@improvedpharma.com or explore how we improve pharmaceutical methods, formulations, and processes.

Author: Stephan Parent, Solid-State Pharmaceutical Research Advisor at Improved Pharma. This article has been adapted from Solid-State Properties of Pharmaceutical Materials by Byrn, Zografi, and Chen (Wiley, 2017).

  1. Henck J.-O.; Griesser, U.; Berger, A. Polymorphie von Arzneistoffen – Eine wirtschaftliche Herausforderung? Die Pharmazeutische Industrie 1997, 59 (2), 165–169.
  2. Cruz-Cabeza, A. J.; Reutzel-Edens, S. M.; Bernstein, J. Facts and Fictions about Polymorphism.Chemical Society reviews 2015, 44 (23), 8619–8635. https://doi.org/10.1039/c5cs00227c
  3. Threlfall, T.L. Analysis of Organic Polymorphs. A Review. The Analyst 1995, 120 (10), 2435–2460. https://doi.org/10.1039/AN9952002435
  4. Grant, D. J. W. Theory and Origin of Polymorphism. InPolymorphism in Pharmaceutical Solids; Brittain, H. G., Ed.; Marcel Dekker: New York, 1999; pp. 1–33.
  5. Burger, A.; Ramberger, R. On the Polymorphism of Pharmaceuticals and Other Molecular Crystals. I.Mikrochimica Acta 1979, 72 (3-4), 259–271. https://doi.org/10.1007/bf01197379.
  6. Burger, A.; Ramberger, R. On the Polymorphism of Pharmaceuticals and Other Molecular Crystals. II.Mikrochimica Acta 1979, 72 (3-4), 273–316. https://doi.org/10.1007/bf01197380.
  7. Giron, D. Thermal Analysis and Calorimetric Methods in the Characterization of Polymorphs and Solvates.Thermochimica Acta 1995, 248, 1–59. https://doi.org/10.1016/0040-6031(94)01953-e.
  8. Burger, A. Dissolution and Polymorphism of Metolazone.Arzneimittel-Forschung 1975, 25, 24–27.
  9. Grant, D. J. W.; Brittain, H. G. Solubility of Pharmaceutical Solids. InPhysical Characterization of Pharmaceutical Solids; Marcel Dekker: New York, 1995; pp. 322–326.
  10. Yu, L. Inferring Thermodynamic Stability Relationship of Polymorphs from Melting Data.Journal of Pharmaceutical Sciences 1995, 84 (8), 966–974. https://doi.org/10.1002/jps.2600840812.
  11. Chauvet, A.; Masse, J.; Ribet, J.-P.; Bigg, D.; Autin, J.-M.; Maurel, J.-L.; Patoiseau, J.-F.; Jaud, J. Characterization of Polymorphs and Solvates of 3-Amino-1-(M-Trifluoromethylphenyl)-6-Methyl-1H-Pyridazin-4-One.Journal of Pharmaceutical Sciences 1992, 81 (8), 836–841. https://doi.org/10.1002/jps.2600810824.
  12. Landgraf, K.-F.; Olbrich, A.; Pauluhn, S.; Emig, P.; Kutscher, B.; Stange, H. Polymorphism and Desolvation of Flupirtine Maleate.European Journal of Pharmaceutics and Biopharmaceutics 1998, 46 (3), 329–337. https://doi.org/10.1016/s0939-6411(98)00054-x.
  13. Behme, R. J.; Brooke, D.; Farney, R. F.; Kensler, T. T. Characterization of Polymorphism of Gepirone Hydrochloride.Journal of Pharmaceutical Sciences 1985, 74 (10), 1041–1046. https://doi.org/10.1002/jps.2600741004.
  14. Zhang, G. G. Z.; Gu, C.; Zell, M. T.; Burkhardt, R. T.; Munson, E. J.; Grant, D. J. W. Crystallization and Transitions of Sulfamerazine Polymorphs.Journal of Pharmaceutical Sciences 2002, 91 (4), 1089–1100. https://doi.org/10.1002/jps.10100.
  15. He, X.; Griesser, U. J.; Stowell, J. G.; Borchardt, T. B.; Byrn, S. R. Conformational Color Polymorphism and Control of Crystallization of 5‐Methyl‐2‐[(4‐Methyl‐2‐Nitrophenyl)Amino]‐3‐Thiophenecarbonitrile.Journal of Pharmaceutical Sciences 2001, 90 (3), 371–388. https://doi.org/10.1002/1520-6017(200103)90:3<371::AID-JPS12>3.0.CO;2-N.
  16. Caria, M. R.; Mohamed, R. Positive Identification of Two Orthorhombic Polymorphs of Sulfamerazine (C11H12N4O2S), Their Thermal Analyses and Structural Comparison.Acta Crystallographica Section B Structural Science 1992, 48 (4), 492–498. https://doi.org/10.1107/s0108768192000910.
  17. Grunenberg, A.; Henck, J.-O.; Siesler, H. W. Theoretical Derivation and Practical Application of Energy/Temperature Diagrams as an Instrument in Preformulation Studies of Polymorphic Drug Substances.International Journal of Pharmaceutics 1996, 129 (1-2), 147–158. https://doi.org/10.1016/0378-5173(95)04283-0.
  18. Cassel, R. B.; Behme, R. A DSC Method to Determine the Relative Stability of Pharmaceutical Polymorphs.American Laboratory 2004, 36, 26-29+10.
  19. Gu, C.-H.; Young, V.; Grant, D. J. W. Polymorph Screening: Influence of Solvents on the Rate of Solvent-Mediated Polymorphic Transformation.Journal of Pharmaceutical Sciences 2001, 90 (11), 1878–1890. https://doi.org/10.1002/jps.1137.